作者:happyfly
2022-10-30
背景
硬件环境:
前10万盘:
Memory 255GiB
Processor Intel(R) Xeon(R) Gold 5218 CPU @ 2.30GHz
GPU GeForce RTX 3090 (前2/3时间用的是3060)
10万盘之后:
Memory 16GiB
Processor Intel® Core™ i7-12700F
GPU GeForce RTX 3060Ti
软件环境:
前10万盘:
Linux Red Hat 4.8.5-36
Python 3.7.13
TensorFlow 1.15
CUDA 11.1
conda 4.12.0
10万盘之后:
Ubuntu 22.04
Python 3.8.13
TensorFlow 1.15 (Novidia)
CUDA 11.7
AI程序:
Katago(曹国梁改进版,规则改为道棋。git clone https://github.com/gcao/KataGo.git)
参数设置为b20c256,由于Katago默认训练结果可用于不同大小棋盘,为了更有针对性,把16路棋盘的权重设为1。
数据:
本次训练一共获得了128个models,总棋局大于26万。
贴子
Katago为了避免贴目偏好,训练过程中贴目的大小都是随机的。分析棋局时,首先读取sgf文件中KM[]和RE[]中的数据,计算出不贴目时黑棋的净剩目数,再用0-9.5贴目分别计算黑棋赢棋的概率(扣除了和棋)。获得的结果以纵坐标为黑棋赢率、横坐标为训练过程,展示在图1中。
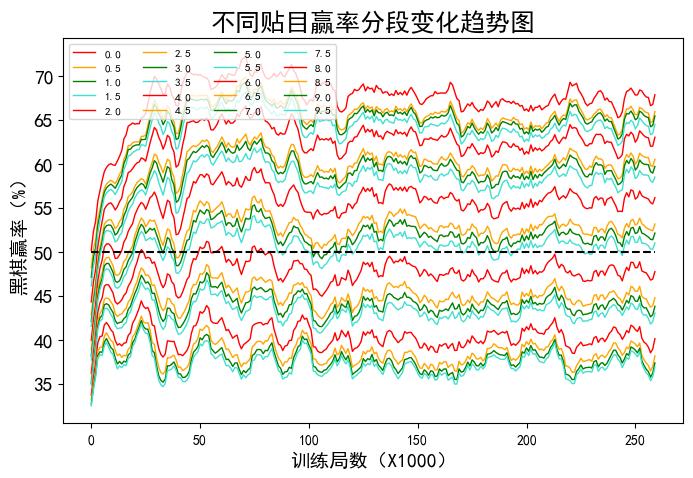
图1
如果随训练进行,把历史棋局累加,不同贴目赢率变化如图2所示:
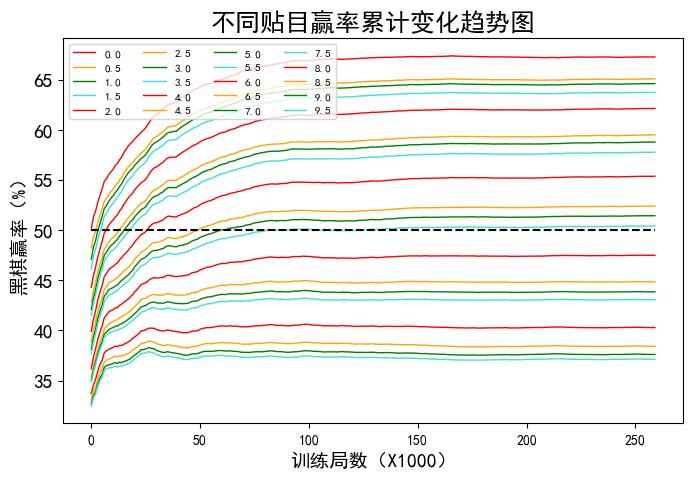
图2
从图中可以看出,离黑棋50%赢率最近的贴目是5.5,换算成贴子的话就是贴2.75子。就是说,对于16路道棋,整个棋盘一共256个点,黑棋获得256/2 +2.75 = 130.75个点为和棋,大于此数赢、小于此数输。
布局
用同样的方法分析了相对于第一手黑棋,第二手白棋出现位置的概率。
由于道棋存在诸多的对称轴,所以第二手可能的位置只有44个,如果白棋是随机落子的话每个位置出现的平均概率是2.27%。靠近平均概率的点不是AI所倾向的。
训练开始时,第二手白棋几乎是随机的。随训练进行,白棋迅速靠近第一手黑棋,然后逐渐远离。白棋选点随训练变化如图3所示:
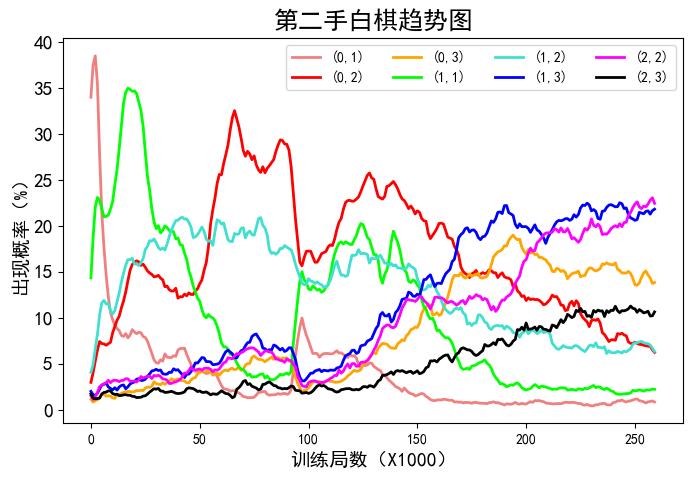
图3
动态变化如图4所示:
图4
从图3的变化趋势看,随训练进行,第二手白棋选点还可能会发生变化,但到目前为止,白棋的分布距离黑棋大约是一个圆形区域(图5)。
图5
总结
没什么可以总结的,数据是客观的。
下面是训练前64个models时写的分析。随训练继续进行,很多结论都发生了变化。这个分析保留在这里,仅供参考。
作者:happyfly
2022-09-06
背景
硬件环境:
Memory 255GiB
Processor Intel(R) Xeon(R) Gold 5218 CPU @ 2.30GHz
GPU GeForce RTX 3090 (前2/3时间用的是3060)
软件环境:
Linux Red Hat 4.8.5-36
Python 3.7.13
TensorFlow 1.15
CUDA 11.1
conda 4.12.0
AI程序:
Katago(曹国梁改进版,规则改为道棋。git clone https://github.com/gcao/KataGo.git)
参数设置为b20c256,由于Katago默认训练结果可用于不同大小棋盘,为了更有针对性,把16路棋盘的权重设为1。
训练过程:
每轮训练生成1000个棋局,训练一轮平均耗时8小时。用了一个月的时间,训练93轮,获得了64个成功的model。从图1可以看出,随着训练的进行,被拒绝的model越来越多,说明越往后训练的难度越大。

图1
数据分析:
整个训练一共获得了100810个棋局,由于最后一个成功的model没有自我对弈的数据,所以单独生成了若干棋局追加到后面,一并作为数据源。有些棋局第一手黑棋弃权,有些第二手白棋弃权(真搞不明白AI是怎么想的),这些棋局都从总棋局中剔除。
由于道棋历史对弈数据匮乏,所以AI训练产生的数据非常珍贵。通过对这些数据分析,可以科学地设置合理的道棋贴子数量,也可以获得道棋均衡的开局方式。
在分析过程中,既要降低数据颗粒性带来的噪音,又要让数据趋势不被均值掩盖,通过摸索,最后设置对数据扫描的窗口为5000局,步长为1000局。总共使用数据为107000局。
贴子
注:道棋采用贴子,为了便于叙述,下面涉及Katago时都表述为贴目,最后换算为贴子。
Katago为了避免贴目偏好,训练过程中贴目的大小都是随机的。分析棋局时,首先读取sgf文件中KM[]和RE[]中的数据,计算出不贴目时黑棋的净剩目数,再用0-9.5贴目分别计算黑棋赢棋的概率(扣除了和棋)。获得的结果以纵坐标为黑棋赢率、横坐标为训练过程,展示在图2中。
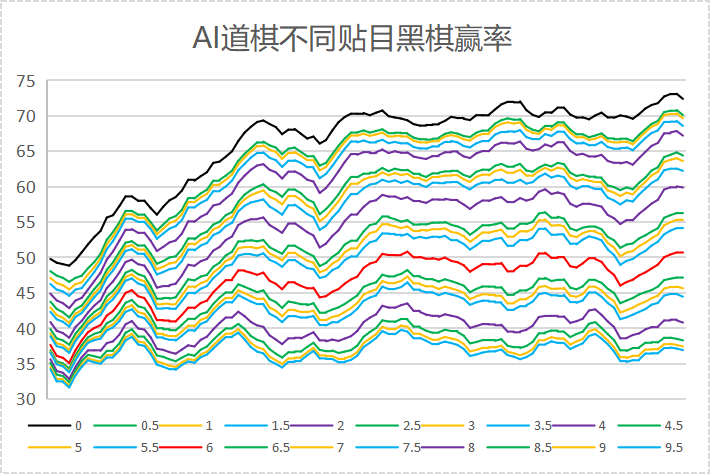
图2
从图2中可以看出,训练刚开始时,贴目0黑棋赢率即为50%(黑线),说明在极低水平时,先手并不能给黑棋带来更多的利益。另外,开始时贴目0-9.5赢率数据非常集中。这是因为最初的AI水平有限,输赢都在十几目以上,几目的贴目很多时候不影响最终胜负结果。随着训练的进行,对应50%赢率的贴目数开始增加,这点和围棋的贴目历史是一致的,从最初的无贴目,到后来的小贴目,再到现在的大贴目。
大约在50000局后,黑棋50%赢率基本上落在6目线上(红线),并且非常稳定。这说明16路道棋的合理贴目是6目,换算成贴子的话就是贴3子。就是说,对于16路道棋,整个棋盘一共256个点,黑棋获得256/2 +3 = 131个点为和棋,大于此数赢、小于此数输。
这里还有一个比较有趣的现象,偶数贴目与±0.5目的胜率相差明显,而奇数贴目与±0.5目的胜率没有显著区别。造成这种现象的原因是这样的:
1、整数贴目都存在和棋,其中奇数贴目的和棋来源于有眼双活造成的和棋,偶数贴目的和棋来源于自然发生。
2、有眼双活和棋的出现概率低于自然发生的和棋。
3、整数贴目±0.5目变成非整数贴目,本质上是把和棋归给谁,-0.5目和棋归黑方、+0.5目和棋归白方。
这种不同贴目对应赢率的不均衡是行棋规则造成的。这个现象也存在与围棋中,由图2可以看出,围棋日本规则贴6.5目与中国规则贴7.5目,其差别没有想象中的大。这也解释了为什么用中、日不同贴目时,结果不一致的概率非常低。
图3是用训练获得的最后一个model自我对弈生成的15000个棋局计算的贴目赢率。对照这些数据就很容易理解不同贴目赢率变化的本质原因了。
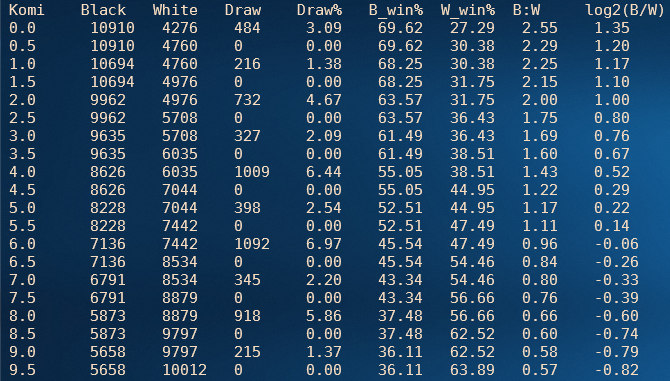
图3
回到道棋,16路道棋合理贴目恰好赶上偶数了,此时无论贴目+0.5还是-0.5都是相当不公平的。最好的办法就是认可和棋的存在。
小结:16路道棋的合理贴子为3子,即黑棋终局131子为和棋,大于此数黑赢,小于此数黑输。
布局
用同样的方法分析了相对于第一手黑棋,白棋出现位置的概率。
由于道棋存在诸多的对称轴,所以第二手可能的位置只有44个,如果白棋是随机落子的话每个位置出现的平均概率是2.27%。靠近平均概率的点不是AI所倾向的。
经过统计,我们发现如下这些点曾经或最终显著高于平均概率,它们是:
(0,1)靠,(02)跳,(03)二间跳,(1,1)尖,(1,2)小飞,(1,3)大飞、(2,2)象步飞
从图4中可以看出,刚开始训练时,AI毫无章法,落子几乎是随机的。很快AI就发现如果要赢棋,必须要杀气,最有效的办法就是靠上去。图中红线所示的“靠”迅速成为了AI看好的点。然而,一旦对手也进化出了如此的智慧,形势急转直下,因为对杀的话后手白棋大亏。随着训练,“靠”迅速衰落。与“靠”同期被看好的还有黄线所示的“尖”。“尖”既能迅速靠近黑棋,又不至于被黑棋反杀,在“靠”衰落之后崛起了,但终究还在“跳”和“小飞”的稳步增长中跌落圣坛,最后和“靠”一样,降到了平均概率,不被AI看好。
中间慢慢上升的是“跳”和“小飞”。“小飞”(深绿线)上升后,一直稳定在20%概率线附近,没有大起大落,说明“小飞”是一个易于掌握且没有明显缺点的位置。“跳”(浅绿线)不一样,在整个训练过程中出现了两次明显的陡升,似乎AI忽然想出了某个有利于“跳”的后续策略。无论如何,在本次训练完成时,“跳”是最优选的位置。
还有三个点概率缓慢且坚定地上升,到最后都超过了平均概率,它们是“二间跳”(深蓝线)、“大飞”(紫线)和“象步飞”(浅蓝线)。
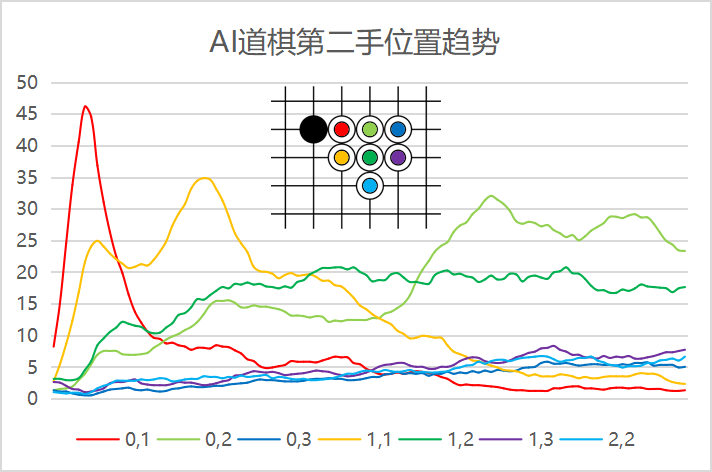
图4
前面提及的七个点,按照它们距离黑子的距离排序:(0,1)靠<(1,1)尖<(02)跳<(1,2)小飞<(2,2)象步飞<(03)二间跳<(1,3)大飞。AI在训练过程中最先发现的近距离优势,马上又发现近距离劣势,在经过大量棋局验证后,认为最佳距离是“跳”,其次是“小飞”,再次是“二间跳”、“大飞”和“象步飞”。
用训练获得的最后一个model自我对弈生成的15000个棋局进行统计,不同位置白棋的概率如下:
(0, 2) 23.6 (1, 2) 17.4 (1, 3) 7.5 (2, 2) 6.5 (0, 3) 5.3 (2, 3) 3.2 (1, 1) 2.6 (6, 7) 2.5 (5, 7) 2.2 (4, 7) 1.7 (5, 6) 1.6 (1, 4) 1.5 (6, 8) 1.3 (0, 1) 1.3 (7, 7) 1.3 (3, 7) 1.3 (7, 8) 1.3 (4, 6) 1.2 (2, 7) 1.1 (2, 4) 1.1 (5, 8) 1.0 (4, 8) 1.0 (0, 4) 0.9 (1, 7) 0.9 (3, 6) 0.8 (6, 6) 0.8 (4, 5) 0.7 (3, 8) 0.7 (3, 4) 0.7 (2, 6) 0.7 (3, 3) 0.6 (2, 8) 0.6 (1, 6) 0.6 (1, 8) 0.6 (2, 5) 0.6 (5, 5) 0.6 (1, 5) 0.5 (3, 5) 0.5 (0, 7) 0.4 (0, 6) 0.3 (0, 5) 0.3 (4, 4) 0.3 (0, 8) 0.3 (8, 8) 0.2
根据这些数据做的概率分布图如下(图5),白色圆形的面积代表了该点出现白棋的相对概率。这个分布挺有意思的,隐约看到了波函数……
图5
小结:第二手优选点 跳 >小飞 >> 大飞 ≈ 象步飞 ≈ 二间跳
总结
AI为道棋理论的建立提供了重要的基础数据,让道棋在短时间内获得了合理的贴目和行棋策略。AI的重要性之于道棋,无论怎么说都不过分。
目前还不清楚此次训练出的model实力如何,但从图4的曲线图可以做一点超前的推测。“跳”是目前白棋最好的应手,但从曲线的变化趋势看,它有没有可能是另一个“尖”呢?就是说,随着训练的延长,最终“跳”的重要性会降低。这种可能性是完全存在的。再深入想想,世界上本来就没有绝对真理。所谓的最佳布局,需要与棋手的水平相对应。水平低的时候,“尖”就是最好的。“跳”和“小飞”你根本就把控不了。用哲学的说法就是:生产关系必需适应生产力的发展水平。
等计算机空闲下来,计划再训练几十个周期,看看是否如同我推测的那样。
为了方便研究,用最后model自我对弈的1000个棋局已经上传到【资料下载】。